Observatoire international des e-fuels, édition…

L'optimisation est surtout utilisée pour planifier et mettre en place des organisations, une autre application moins connue est son utilisation en tant qu'outil d'aide à la décision en temps réel lors de perturbation imprévisible. Voici ici un exemple avec l'industrie du transport maritime de conten

Le transport maritime de marchandise est une industrie complexe qui relie des fournisseurs et leurs clients dans le monde entier grâce au transport maritime de conteneurs à travers un réseau de distribution hautement optimisé. Ces entreprises exploitent des réseaux de transport de marchandises d'un point à un autre du globe au moyen de navires de grande capacité appelés porte-conteneurs. Dans les années 60, l'innovation de la conteneurisation a eu un énorme impact sur l'industrie et a révolutionné le marché de l’import-export de marchandises en réduisant drastiquement les coûts via l’augmentation des quantités de marchandises transportées par voyage.
Aujourd'hui, la quasi-totalité du commerce maritime se fait de cette manière et il apparait donc évident que des solutions de digitalisation associées à des modélisations mathématiques émergent et se concentrent principalement sur ce point tant des gains économiques et environnementaux sont directement accessibles et mesurables.
Un tel dispositif de transport nécessite que les marchandises soient regroupées dans des conteneurs et embarquées sur des navires de grande capacité. Ensuite, les navires et les conteneurs circulent sur un réseau composé de routes de navigation exploitées par des compagnies maritimes et de ports de commerce. Le plus souvent, le trajet d'un conteneur de son origine à sa destination est composé de plusieurs navires consécutifs lui permettant d'atteindre le lieu de sa livraison finale. Le processus de chargement et de déchargement des conteneurs d'un navire à un autre est connu sous le nom de transbordement.
L'un des problèmes les plus critiques auxquels les compagnies de transport maritime doivent faire face chaque jour et qui jusqu’à présent n’a jamais été automatisé, est la gestion de recouvrement de perturbations imprévisibles. Il y a perturbation imprévisible lorsqu'un ou plusieurs navires sont retardés, ces événements perturbateurs sont très difficiles à prédire sur le long terme (grèves, tempêtes, panne, …), ce qui entraîne des écarts importants par rapport à la planification opérationnelle du réseau. Non seulement le navire concerné est retardé, mais aussi un certain nombre de navires adjacents dans le réseau sont touchés par effet domino, ceci découlant directement des transbordements prévus aux ports suivants la perturbation. Le respect des délais de livraison de ces marchandises est donc directement impacté et représente une menace pour l’entreprise en termes de satisfaction client et donc de perte de part de marché au profit de concurrents plus ponctuels.
Il devient complexe pour un œil humain d'identifier, dans un court délai, la meilleure décision compte tenu de la complexité du réseau mis en place. Les entreprises de transport se doivent donc de prendre des mesures immédiates afin de limiter les dommages de ces perturbations sur leurs services. C'est à ce moment précis qu'intervient la recherche opérationnelle ou autrement appelée l’optimisation mathématique. La modélisation du réseau et des actions de recouvrement potentielles sous forme de graphe permet aux opérateurs de s'appuyer sur un outil non subjectif et mathématique donnant des résultats quantifiés dans un laps de temps court. Cet article présente la modélisation mathématique appliquée à un cas pratique pour guider une compagnie de transport maritime de marchandises à se remettre de perturbations imprévisibles impactant son réseau.
Lorsqu'un navire est retardé, des décisions doivent être prises rapidement pour limiter l'impact de la perturbation et maintenir les horaires prévus tout en minimisant les frais supplémentaires. De nombreuses solutions existent, comme raccourcir les temps à quai ou même l’insertion d’un bateau attendant à quai afin de récupérer les conteneurs en attente, mais les solutions les plus récurrentes sont les suivantes, ce seront celles-ci que le modèle considèrera :
Le modèle à développer doit prendre en compte l’aspect spatial (déplacement d’un bateau entre différents ports pour délivrer sa marchandise) et temporel (planning à respecter sous peine de faire rater sa correspondance à un conteneur) du problème.
Une première façon de modéliser le problème sous forme de graphe consiste à prendre comme objets d’étude les navires, les conteneurs, les ports et considérer chaque nœud du graphe comme étant la position d’un navire, dans un port donné, à un instant donné. Un arc représentant le voyage du bateau considéré entre deux positions à une vitesse donnée.
Un problème de perturbation de ce type soulève la question suivante : comment se remettre d’une perturbation pour ramener l’ensemble des navires concernés au planning initial tout en réduisant les coûts associés et en respectant les contraintes physiques imposées. Un cadre d’étude se doit d’abord d’être fixé, chaque problème comprend un sous-ensemble de navires susceptibles d'être touchés par la perturbation, et sont supposés supporter le transbordement des conteneurs retardés sur les ports suivant la perturbation. Le champ d'application est ensuite défini géographiquement par les navires considérés, leurs positions et leurs routes potentielles, et enfin temporellement par un horizon temporel défini obligeant les navires à récupérer avant un certain délai fixé (un horaire de passage groupé obligatoire pour les navires d’une même compagnie par le canal de Suez par exemple). Ce cadrage limite la complexité et réduit le modèle à ce qui est réellement touché par la perturbation.
Le modèle se base donc sur un graphe temporel dirigé où les nœuds sont associés à un triplet (navire, port, instant) et les arcs définissent les segments réalisables de toutes les routes potentielles des navires à travers le réseau selon le scénario de recouvrement.
A l'exception des nœuds initiaux et finaux qui sont figés par les conditions initiales et les contraintes d'horizon temporel, tous les autres nœuds sont multiples car ils représentent des solutions de navigation à différentes vitesses et sur différentes routes (en raison de l'omission ou du saut des options de recouvrement des ports). Tout cela définit un graphique temporel dirigé qui représente le réseau de transport maritime de ligne. Sous cette modélisation simple, il y a autant de sous-graphes indépendants qu'il y a de navires. Il s'agit alors de trouver le chemin le plus court pour tous les navires considérés.
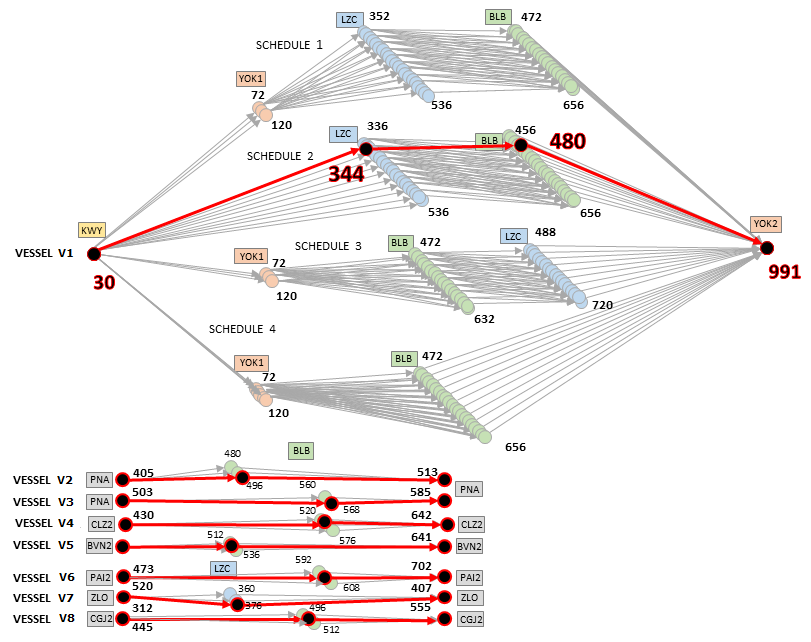
Figure 1: Cas du retard du bateau « V1 » En rouge sont représentées les solutions optimales identifiées par le modèle : Saut du port YOK1 et accélération du bateau sur son chemin jusqu’au port final YOK2.
Remarque au lecteur : dans cette modélisation, le choix a été fait volontairement de dupliquer certains nœuds dont le scenario diffère (Sur la Figure 1, le nœud (V1,LZC,352) par exemple existe pour le scenario 1 et 2, et le nœud (V1,LZC,536) pour les scenarios 1,2 et 3). Ce choix est questionnable de par l’augmentation du nombre de variables à considérer par le modèle par la suite, mais il permet aussi de ne pas imposer de contrainte de scenario au sein du modèle mathématique comme aucun arc ne lie les nœuds de scénarios différents, et donc de réduire significativement le nombre de contraintes à considérer. C’est cette deuxième option qui a été priorisée.
Après le réseau, l’étape la plus importante consiste à fixer les coûts et donc la fonction objective du problème que le modèle cherchera à minimiser. L'idée de recourir à la Recherche Opérationnelle est d'aider à résoudre un problème décisionnel complexe entre les principaux coûts entrant en jeu :
Suite à l'analyse de premiers résultats, cette modélisation présente de bonnes performances et a prouvé son efficacité sur de nombreux cas concrets où le modèle apporte une solution au moins aussi bonne que celle prise par les opérateurs lorsque la situation s’est présentée en direct. Cependant, elle présente de nombreuses failles, la plus évidente concerne le cas du recouvrement des conteneurs retardés ou ayant raté leurs connexions. En effet, actuellement le modèle ne permet pas de regénérer un planning pour les conteneurs ayant été retardés ou déconnectés, ceux-ci sont simplement considérés par une pénalité au sein de la fonction objective et sortent du modèle sans avoir de proposition de recouvrement. Il apparait donc évident que la modélisation sous forme de graphe se doit d’intégrer une nouvelle instance dans sa modélisation : les conteneurs.
Comme décrit précédemment, la fonction objective du problème mathématique modélisant la somme des coûts à minimiser, tient compte des coûts de carburants et des coûts fictifs de pénalité en cas de retard ou de mauvaise connexion de la cargaison. Les instances modélisées sont soumises à des contraintes assurant la faisabilité de la solution générée :
Le principal inconvénient dans la modélisation précédente est qu'elle ne tient pas compte du réacheminement des conteneurs. En d'autres termes, lorsqu'un conteneur est gravement retardé ou, pire, manque une connexion, le modèle considère qu'il ne sera pas livré et le fait sortir de la modélisation. Aucune option de recouvrement n'est envisagée pour le faire livrer, alors que dans la réalité, il ne sera pas abandonné mais chargé sur un autre navire et suivra un voyage non planifié jusqu'à sa destination finale. On pourrait donc s'attendre légitimement à ce qu'un outil d'optimisation incorpore cette fonctionnalité. Le modèle suivant répond à cette problématique.

Figure 2: un exemple de réacheminement d'un conteneur. Le bateau A est incapable d’assurer son transbordement au port P2, il accélère afin de l’effectuer sur le port P3 avec le bateau C et assurer la livraison des conteneurs au port P4, en retard.
Afin de modéliser les conteneurs en tant qu'objets au sein du réseau, nous avons dû adapter notre modélisation sous forme de graphique. Différents arcs et nœuds supplémentaires ont été créés pour les conteneurs afin d’intégrer leurs caractéristiques particulières de déplacement spatial au sein du graphe. Les conteneurs ne sont plus considérés comme des objets liés aux navires, mais comme des objets, libres de passer d'un navire à un autre à condition que les deux navires fassent escale dans le même port et le premier avant le second. Les conteneurs entrent également dans le réseau par des nœuds « gate » reliés aux premiers et derniers appels de port (qui sont fixes et connus). Des arcs de non-connexion sont aussi créés, entre ces nœuds « gate », ceux-ci sont pondérés avec le coût de la mauvaise connexion reliant ces nœuds « gate » pour chaque groupe de conteneurs. Toutes ces nouvelles caractéristiques du graphe ajoutent de la complexité au problème puisque les deux flux de navires et de conteneurs sont traités en parallèle. Il s’agit d’un problème d’optimisation dit « Multi-flow ».
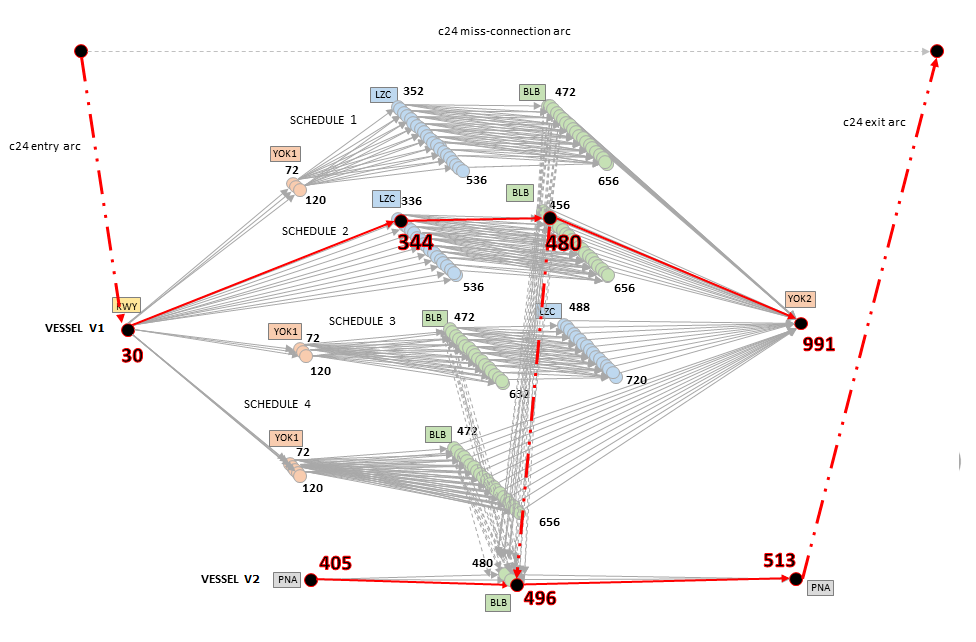
Figure 3 : Cas du bateau « V1 » avec un seul groupe de conteneurs « c24 » En rouge sont représentées les solutions optimales du modèle avec les arcs pleins représentant la route du bateau et en pointillés le groupe de conteneurs c24 considéré.
Les algorithmes des deux modèles ont été exécutés pour chaque cas d'utilisation. Les solutions et les performances ont été comparées et confrontées aux décisions réelles qui avaient été prises par les agents opérationnels. Tout d'abord, il convient de mentionner que les deux modèles ont fourni des solutions au moins aussi bonnes que celles choisies lors des cas pratiques. Pour certains, les décisions prises par les agents étaient optimales selon le modèle, pour d’autres, l'utilisation des deux modèles aurait permis de mieux conseiller les agents et économiser des dépenses de recouvrement du planning. Les deux modèles ont donné les mêmes solutions pour les quatre cas d'utilisation puisqu'il n'y avait pas de place pour le réacheminement du fret dans aucun des cas d'utilisation. Afin d'évaluer la performance du nouveau modèle, la méthode de sélection des navires à intégrer à la simulation se doit d’être repensée afin d’ajouter des navires capables de proposer d'autres itinéraires pour les conteneurs retardés afin de mieux évaluer les solutions de réacheminement des marchandises.
Lors de cette étude, un autre cas d'utilisation a été élaboré pour tester les avantages potentiels de l’intégration du réacheminement des conteneurs. En partant des cas utilisés pour le premier modèle, les données ont été légèrement modifiées en ajoutant des navires supplémentaires offrant une route alternative pour atteindre la destination finale. Les résultats ont été satisfaisants puisque le second modèle modélisant les conteneurs propose d’en réacheminer certains, alors que le premier les considère simplement comme des conteneurs retardés ou non connectés. Le second modèle s'est avéré satisfaisant pour proposer de meilleurs résultats que le premier à condition qu'un réseau plus large soit considéré par le modèle, de sorte que toutes les actions de recouvrement possibles pour les navires et les conteneurs soient parfaitement évaluées.
La Recherche Opérationnelle sert ici d’accélérateur puissant d’aide à la décision, l’ensemble des options modélisées sont évaluées et comparées analytiquement sur leurs coûts estimés et l’optimum est mis en avant. Cette méthode reste un outil puissant de prétraitement des données selon un paramétrage en entrée et n’a pas vocation à remplacer les décisions d’un opérateur humain. Celui-ci peut alors évaluer de manière plus fine la faisabilité en pratique d’une solution optimale théorique proposée par l’outil et changer les paramétrages selon ses observations afin d’en déduire la meilleure décision à prendre.
Cette étude s'appuie sur le travail réalisé par Alexandre Orhan et Florian Binter sur la gestion des perturbations en transport maritime.
Si vous souhaitez en savoir plus sur nos solutions d'IA, rendez-vous sur notre site web Heka
Contact : david.martineau@sia-partners.com